What is Stress concentration?
Mechanical elements such as shafts, gears, support brackets threaded fasteners, etc often have 3D features that change their size and shape to fulfil their purposes such as stepped shaft shoulder for ball bearing, shaft keyways for keys, grooves for retainer rings, and O-rings.
These sudden change geometry points under its load conditions often create localized stress fields where the part typically fails. This localized stress is called Stress concentration and those features are sometimes referred to as Stress concentrators or stress raisers or risers.
What is the Stress concentration factor?
A stress concentration factor, normally denoted as Kt quantifies the stress concentration in a part and is defined as the ratio of the maximum stress to the nominal or reference stress.
Kt = σmax/σnom
Nominal stress (σnom) is the stress without the stress concentrators such as grooves while the maximum stress (σmax) is the maximum stress with the stress raiser feature.
Stress concentration factor
Stepped shaft with fillet
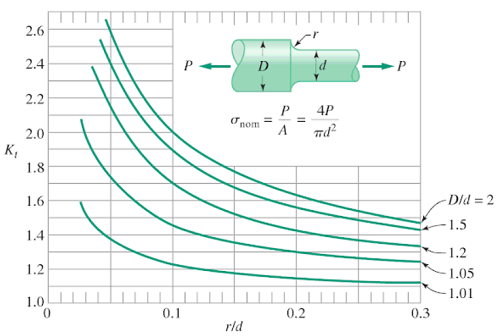
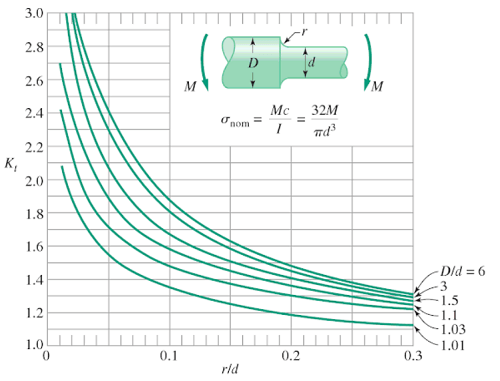
References and recommended reading
- Collins, J. (2010). Mechanical design of machine elements and machines. Hoboken, NJ: Wiley
- Pilkey, W. D.(2005). Formulas for stress, strain and structural matrices 2nd Edition John Wiley & Sons
- Roark’s Formulas for Stress and Strain, 9E (MECHANICAL ENGINEERING)
- Stress concentration. (2022, May 8). In Wikipedia. https://en.wikipedia.org/wiki/Stress_concentration
